The ongoing rise in infectious diseases globally creates an ever-increasing need for new technologies in laboratory automation. Improvements in machine design enable more reliable and more accurate test results, delivered faster and often at lower overall cost than traditional approaches.
Lab equipment based on hybrid polar/cartesian technology, like Haydon Kerk Pittman’s new Z-Theta™ dual-motion linear actuator, offers significant advantages over traditional cartesian coordinate systems, including flexibility, value, durability, and performance suited for a host of lab automation applications.
 Traditional vs. hybrid: How do cartesian coordinate systems compare to polar/ cartesian systems?
Traditional vs. hybrid: How do cartesian coordinate systems compare to polar/ cartesian systems?
In lab automation, designers have historically formatted sample beds for the cartesian coordinate system using an X-Y or X-X’-Y axes configuration as shown below in Fig. 1(b). While this traditional method is successful, hybrid polar/cartesian systems as shown in Fig. 1(a) offer an increasingly popular and beneficial alternative in lab sample and liquid management.
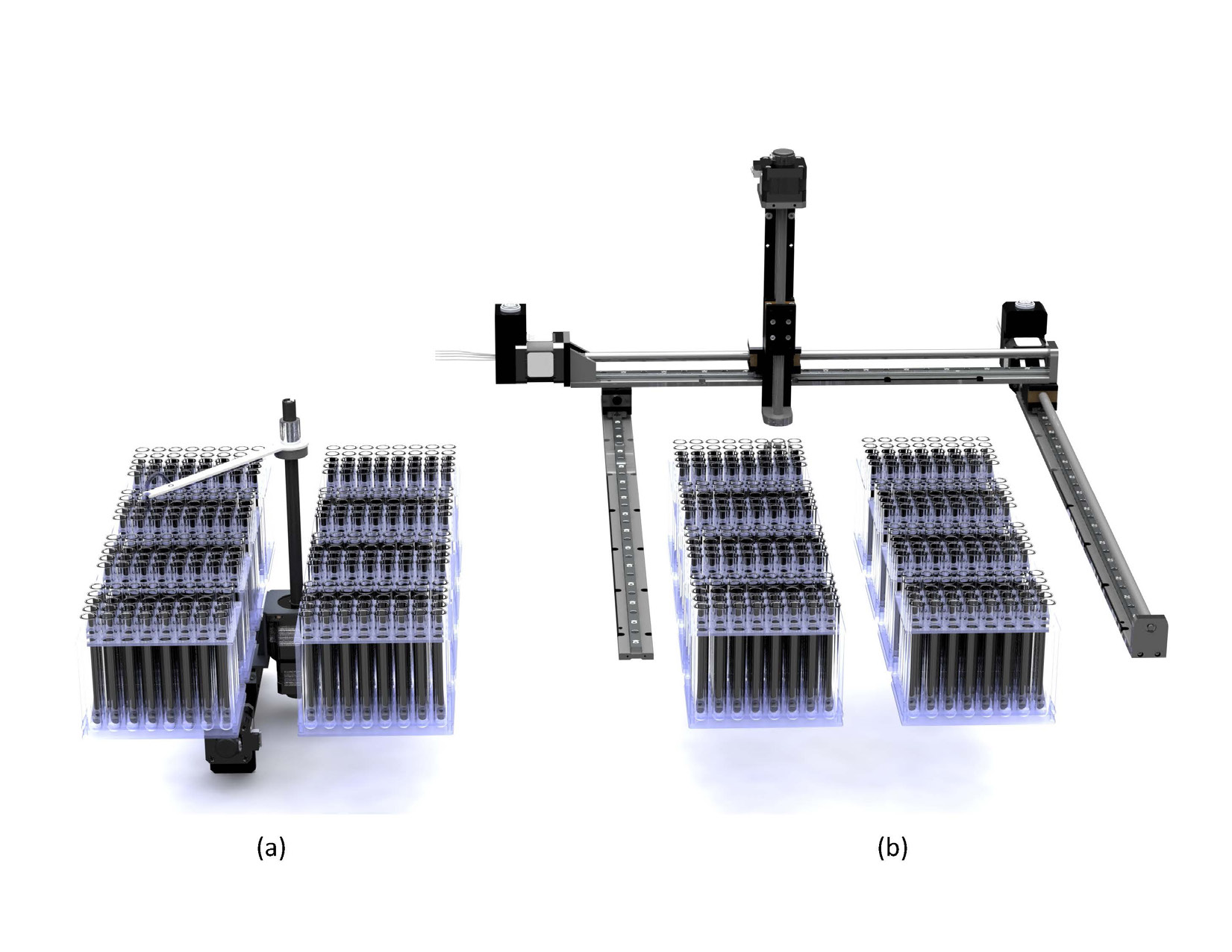
Figure 1: Polar/Cartesian Hybrid vs Cartesian Coordinate System |
How hybrid systems work
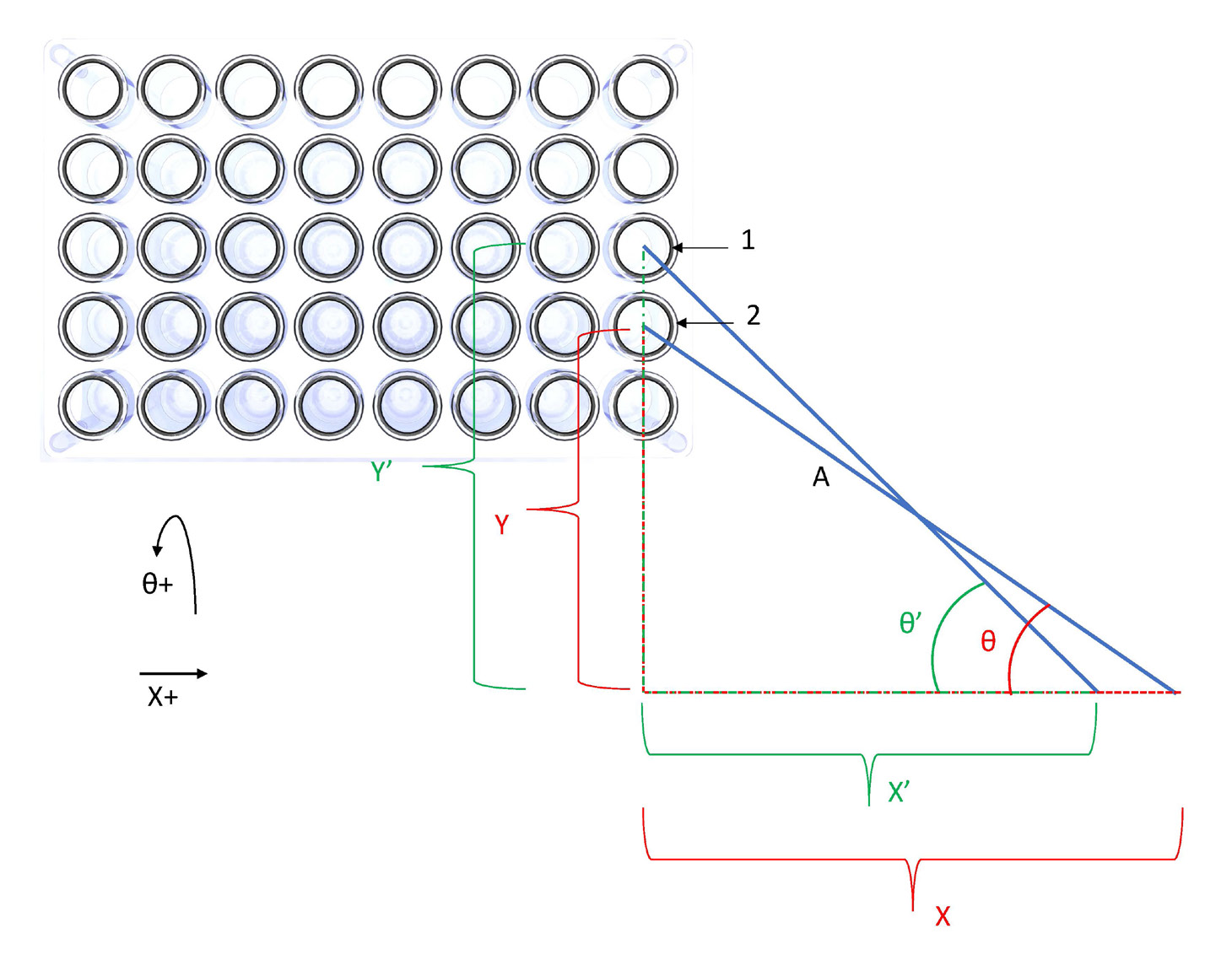
The traditional cartesian method, illustrated in a top-perspective view in Fig. 2, allows simple movement from sample position 1 to position 2. In this figure, blue lines represent a rigid arm like the one shown on the hybrid model in Fig. 1(a).
|
| Figure 2: Theta-X Motion Computation |
| |
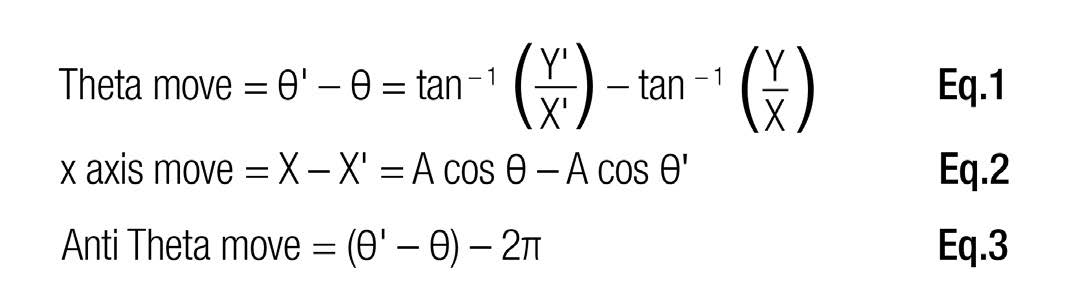 |
By contrast, in a hybrid polar/cartesian coordinate system such as the one shown in Fig. 1(a), the move between sample positions is more complex, involving trigonometry to calculate. However, since the geometries are known, computation is simple. Keeping in mind the positive convention for the theta and x axes, equations Eq.1 and Eq. 2 demonstrate the moves needed to complete the articulation from position 1 to position 2.
In practice, variables Y, Y’, X, X’, and A are known by the physical construction of the machine. Therefore, only θ and θ’ require computation. In this case, if the theta must travel in the negative direction (as defined in Fig. 2), the theta axis command is again noted in Eq. 3.
Creating compact dual motion
Several methods are available to create linear and rotary motion as a part of a singular function. Often, designers select a combination of belts, pulleys, and support bearings to rotate an otherwise purely linear product. While effective, this approach involves more components and additional assembly time than less complex solutions.
Further, belts increase compliance in the system, which can in turn limit overall bandwidth. To reduce the impact of this effect, designers consider two mechanical variations:
Pulley ratio – This ratio is essentially gearing the axis, allowing for reduced inertia reflected to the motor shaft.
The industry-accepted standard for a belt pulley configuration is to fall below a 2:1 ratio. The result of the pulley
ratio is a 4x reduction in the reflected inertia if the original design had a 1:1 ratio. |
| |
Reconfiguring the theta arm – Changing the theta arm can reduce weight as well as shift weight toward the
center of rotation. Because this action impacts rotary inertia, it can also help to improve performance. |
 How can polar/cartesian systems benefit machine design?
How can polar/cartesian systems benefit machine design?
Polar/cartesian systems can benefit machine design in lab automation in several ways, including improving sample integrity, reducing machine footprint, and offering cost savings over alternative methods.
Improved integrity through reduced contamination
Motion control components will generate particulate during basic operation simply from coming into contact with each other and this foreign matter can negatively impact the integrity of test results. Traditional cartesian systems, using components mounted directly over test samples (Fig. 1(b)), carry a risk of sample contamination. Options for guarding or sealing motion devices to mitigate the risk of sample contamination often increase machine size and/or overall cost.
The design of a hybrid polar/cartesian system virtually eliminates this contamination. In contrast with standard cartesian systems, in hybrid systems the rigid arm’s movement is separate from the components with which it has direct contact; therefore, this motion does not produce particulate. The z-axis guide shown in Fig. 1(a) is sliding over the travel path of the x-axis instead of over the samples themselves, further mitigating the risk of foreign debris contaminating a test sample.
Reduced footprint and improved flexibility through efficient use of space
Most sample array equipment is designed to handle large sample sizes like those shown in Fig. 1(a) and 1(b), which include multiple racks of test tubes. However, purely cartesian systems often have a large footprint due to their configuration. The carriage, motor, and end stops consume unusable stroke length, and are compounded by unusable space at the perimeter of the test bed that further adds to the overall size of the unit.
Conversely, the polar/cartesian system’s motion components are largely below the test bed except for the z-axis and theta arm. With this design, the fixed arm is attached to a theta axis that swings over the sample array to address each individual sample, achieving greater flexibility. The component travels through the center of the sample bed, saving space and creating a reduced footprint where the sample bed can run to the limits of the machine’s area. Further, reducing the stroke of the x-axis achieves secondary space savings because the rigid arm articulates through its theta sweep to extend the x-axis reach at either end of the stroke, eliminating lost stroke along the x-axis and reducing cost.
Adding the theta axis to an x-axis for linear translation can effectively replace a purely cartesian X-Y or X-X’-Y system. In each case, a z-axis can be employed as
shown in Fig. 1.
Cost savings through simplicity
With the shorter x-axis as described above and the possibility of using fewer components in overall design, hybrid polar/cartesian systems can achieve significant cost reduction. In the case of Haydon Kerk Pittman’s Z-Theta™ dual-motion platform described below, this savings is as much as 60 percent over traditional purely cartesian coordinate designs.
 What are the advantages of Haydon Kerk Pittman’s Z-Theta™ dual-motion platform?
What are the advantages of Haydon Kerk Pittman’s Z-Theta™ dual-motion platform?
Few existing designs offer a singular device that achieves both rotary and linear motion, and even fewer do so without the use of a belt for the theta axis. Haydon Kerk Pittman’s innovative Z-Theta linear actuator does just that and more.
The Z-Theta, shown in Fig. 3, is a result of focused development, manufacturing expertise, and deep knowledge of rotary and linear motion. Z-Theta features the patented ScrewRail® linear actuator, which combines guidance and linear transmission in a slender co-axial profile. Haydon Kerk Pittman’s unique dual-motion integration with a pair of stepper motors adds rotary (theta) motion in a manner that reduces motion system size by 50-80 percent and provides as much as a 60 percent overall cost reduction when compared to traditional design approaches.
Further customization options include a variety of lead screw resolutions, available freewheeling and anti-backlash nut selections, stepper motor configuration options, and optional encoders for both the linear and rotary axes that allow for either position confirmation or full step-servo control of the device.
The Z-Theta’s highly configurable design provides a full motion solution ideal for easy integration into existing assemblies, and its compact, modular “bolt-in” package allows the benefit of reduced complexity.
See the Z-theta in motion Watch Video
Click here to download PDF version.