In many devices lead screw assemblies are used to convert motion from rotary to linear and vice-versa. Historically, these assemblies have had poor efficiencies and relied on grease for improved performance. Over the past few decades the advent of engineered polymers and new manufacturing capabilities have changed the game for the conventional lead screw assembly making it a powerful solution for motion based design challenges. At first glance lead screw assemblies seem rudimentary, but they are designed to perform a very specific function, and even with the latest developments in materials and manufacturing processes having a basic understanding of how lead screws operate can be the difference between a successful design and catastrophic failure.
To help explain the theory of operation behind lead screws let’s first consider the operation of a basic ramp. The illustration in Figure 1 below shows a person pushing a box up a ramp to raise it from one level to the next. The ramp serves to lift against the force of gravity by transmitting a portion of the person’s horizontal push force into a vertical force. In addition to gravity and the person’s push force there is also a normal force from the ramp and a frictional force between the box and the ramp. Friction is drawn as bi-directional because it always resists the direction of motion which in this case could be up or down the ramp. The frictional force (Ff) is the product of the coefficient of friction between the two sliding surfaces (box and ramp) and the normal force (Fn). In this example there are three factors that will determine how much push force is needed to move the box up the ramp; ramp angle alpha (α), the magnitude of the load, and the coefficient of friction between the box and the ramp. As the ramp angle alpha (α) increases the person needs to apply more push force to move the box up the ramp, but they also need to travel less to achieve the same lift. A large enough ramp angle or a low enough coefficient of friction will allow the box to slide down the ramp if there is no force to oppose it (in a lead screw this phenomenon is known as backdriving).
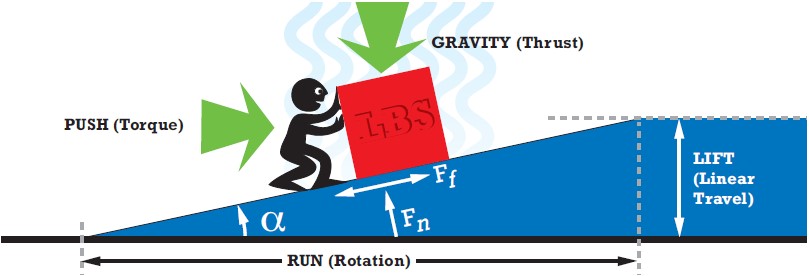 |
| Figure 1: Ramp Illustration. |
The function of a lead screw is to convert rotational motion to linear motion, or rotational force (torque) to linear force (thrust). For conceptual understanding, the thread form geometry of the lead screw can be ignored which simplifies the screw to a ramp that is wrapped around a cylinder, thus creating a helix. In this case the lift becomes the linear motion component of the screw, and run becomes the rotation of the screw as noted in Figure 1. The lead of the screw is defined as the linear distance traveled per rotation of the screw. The gravity component of the diagram becomes the total thrust force provided by the nut traveling on the screw. The person’s push force becomes the torque input that drives the load and alpha becomes the lead angle of the screw.
Properly sizing the lead screw assembly is critical to the success of the application. Defining the total thrust and maximum linear speed required is a good starting point. There are several factors to consider when calculating the maximum thrust required such as acceleration, load, axis orientation, drag forces, etc. The maximum speed can be determined by how much time is available to complete the travel which includes acceleration and deceleration ramps if needed. A factor of safety may be added to both the maximum thrust and speed. In many cases the maximum thrust will narrow the selection of lead screw diameters available as a solution. The critical screw speed (discussed later) may also limit the diameters available. Selecting a lead requires additional information which includes resolution requirements, backdriving considerations, and drive input availability. The resolution of the system is defined by the linear distance traveled per the smallest rotational move achievable (this may not be a factor in some designs). A numerically small lead will provide higher resolution than a larger lead. If the lead screw assembly needs to resist motion when power is lost then it cannot be backdrivable. The ability of the lead screw to backdrive is a function of the lead angle, thread geometry, and coefficient of friction. If a non backdriving lead is needed the manufacturer of the lead screw should be consulted as specific thread geometries may vary as will the coefficient of friction (material dependent). The drive input is typically a motor which is limited by size, availability, budget, and available input power. As the application requirements are defined, a clear performance target of the lead screw assembly can be developed.
Converting the linear thrust and speed into torque and rotational speed is achieved by Equations 1 and 2. Varying the lead will affect both the required torque and speed of the drive input to achieve performance goals. Altering the efficiency will affect the drive torque as can be demonstrated by Equation 1. It is possible to change the lead screw efficiency while keeping the same diameter and lead by altering the coefficient of friction in the assembly. This is commonly done by changing the nut material or adding a coating to the screw.
 |
| Equation 1 |
| |
 |
| Equation 2 |
Proper mounting and alignment of the screw as well as guidance of the load are critical. The mounting configuration contributes to the maximum allowable rotational speed. This can be determined by the simplified critical speed calculation of the screw as shown in Equation 3 which assumes a screw material with a modulus of Elasticity of 28 Mpsi (such as 303 stainless). The mounting factor is one of four unique mounting methods as described in Table 1.
 |
| Table 1: Mounting Configurations. |
Typically the rotational speed of an application is limited to 75% of the critical speed calculated to help account for minor misalignment and manufacturing tolerances. Exceeding the critical speed can cause an unstable condition which can damage the lead screw assembly and other components linked to it.
When using a lead screw assembly with a polymer nut the material’s pressure velocity rating (PV) will need to be considered. Pressure velocity is a property that helps define how much heat generation the material can withstand. The generated heat is caused by the friction between the screw and the nut which is directly related to the thrust force and rotational speed. Exceeding the PV can cause rapid failure of the thread system in a lead screw assembly. There are several ways to reduce the PV of an application such as decreasing the load, decreasing the linear speed, or increasing lead as can be demonstrated by the simplified PV calculation shown in Equation 4.

| Where: |
CS= Critical Speed in RPM |
| |
MF = Mounting Factor |
| |
RD = Root Diameter of the Lead Screw in Inches |
| |
L = Length between Supports in Inches |

| Where: |
PV = Pressure Velocity in psi fpm |
|
LS = Linear Speed in Inches per Second |
|
l = Lead in inches |
|
P = Load in Pounds |
| |
OD = Outside Diameter of the Lead Screw in Inches |
| |
RD = Root Diameter of the Lead Screw in Inches |
There is an assumption made in the pressure velocity calculation that the load P is purely a thrust load on the lead screw nut. This requires proper load guidance by a load bearing member such as a guide rod or ball bearing linear guide rail. It is poor design practice to use a lead screw as both the driving component and load guidance member. The result is off axis loading of the nut which creates a moment load condition as shown below in Figure 2a. Applying a moment load to the lead nut can cause several potential failure methods including mounting, PV, and excessive drag. If the moment load is large enough a mounting failure in the form of fracture can be caused by high stress concentrations at the transition between the mounting feature (thread or flange) and the nut body. All moment loading of the nut will cause localized areas of elevated PV in the thread system. If elevated over the material’s PV rating the thread system may rapidly fail. The PV is elevated due to areas of elevated pressure between the nut and lead screw. The elevated pressure also increases the required torque to drive the screw which can cause stalling or motor failure. When adding a guide element as shown in Figure 2b the moment load is supported by the guide, and not the lead screw. The mounting arm which connects the nut to the guide needs to be reasonably stiff. Alignment of the lead screw and guide member is also critical to proper function and longevity. Excessive misalignment between the screw and guide member will cause binding which will increase PV, drag torque, and potentially stall the motor.
 |
| Figure 2a: Unguided lead screw axis. |
| |
 |
| Figure 2b: Guided lead screw axis. |
 Now that we’ve covered some of the theory let’s put it to practice on an example.
Now that we’ve covered some of the theory let’s put it to practice on an example.
An axis of motion is required to lift a 15 lbs object 12 inches within 3.5 sec. Based on the motion profile and consideration for drag as well as a small margin of safety a maximum linear speed of 4 in/sec with a thrust load of 25 lbs is defined for the lead screw. A “Simple/Simple” (Table 1) screw support geometry is proposed for the design, and due to the length of the lead nut, stroke length requirement, and some margin at either end of stroke the distance between supports is 16 inches. Due to reasonable low positional accuracy requirement, and gravity on the vertical axis that will bias the nut to one side of the thread a standard, or general purpose lead nut is selected (as opposed to an anti-backlash nut). Based on a table for loading and recommended screw diameters listed on the manufacturer’s website a 0.250 inch diameter screw is initially selected. The available motor offers a reasonably flat torque curve of 60 oz-in up to about 650 RPM before quickly dropping off to zero. In a previous design a 0.100 inch lead was used with a 0.250 inch diameter screw and is readily available if it will meet the requirements of the new application. Applying some of the information above to Equation 2 we discover in Equation 5 that the lead is too small for the available motor and target speed of the application. Rearranging Equation 5 into Equation 6 results in the minimum lead needed to use the motor and still meet the required speed. Checking with the manufacture, a 0.500 inch lead is available which results in a rotational speed requirement of 480 RPM as shown in Equation 7. This is within the 650 RPM rated speed of the motor.
 |
| Equation 5 |
| |
 |
| Equation 6 |
| |
 |
| Equation 7 |
With the standard materials of a 303 SS lead screw and acetal based nut the manufacturer specifies an efficiency of 73.1% for a 0.250 inch diameter screw with a 0.500 inch lead. Applying this information as well as the required thrust to Equation 1 results in a required drive torque of 43.5 oz-in as shown in Equation 8 below. This is within the motors capability of 60 oz-in and provides some torque overhead.
 |
| Equation 8 |
Now that a diameter and lead have been selected that meet the speed and thrust requirements of the application when driven by the selected motor the next step is to verify the support configuration and material selection. From the manufacturer’s specification sheet the root diameter of the lead screw is 0.169 inches. With this additional information, and Equation 3, the critical speed of the lead screw configuration is calculated to be 3,103 RPM as demonstrated by Equation 9. To account for misalignment and manufacturing tolerances the critical speed limit is typically set to 75% of the calculated value. Equation 10 shows the critical speed to be 2,327 RPM with a safety factor applied. The maximum speed requirement of the application of 480 RPM is well within the limiting critical speed of the screw configuration.
 |
| Equation 9 |
| |
 |
| Equation 10 |
The desired material for the nut used in this application is acetal based and has a pressure velocity limit of approximately 12,000 psi fpm. Using Equation 4 the pressure velocity with the configuration selected is 8,230 psi fpm as shown in Equation 11. With the basic parameters covered the 0.25 inch diameter screw with a 0.500 inch lead will meet the needs of the application when coupled to the available motor. Another important piece of information in the design of this axis is that the lead is efficient enough to backdrive, and to keep the load from falling under its own weight when power is removed from the motor, a brake will need to be implemented.
 |
| Equation 11 |
There are other topics to consider when designing a lead screw driven axis, but the concepts discussed cover the basics and provide a solid foundation to design a successful lead screw driven axis of motion. Understanding how to properly implement a lead screw into a design will improve the chances of success by avoiding potential design pitfalls. When used properly, lead screws are a powerful tool which can be used in many design solutions that not only solve the need to convert rotary to linear motion, but also significantly improve productivity and motion control precision in large-to-micro scale advanced technology applications.
Click here to download PDF version.